| Пример 2 |
|
В спектре затменной переменной звезды, блеск которой меняется за 3,953 сут, линии относительно их среднего положения периодически смещаются в противоположные стороны до значений в 1,9· 10-4 и 2,9· 10-4 от нормальной длины волны. Вычислить массы компонентов этой звезды.
Данные: (Δλ/λ)1 = 1,9·10-4; (Δλ/λ)2 = 2,9·10-4; Ρ = 3д,953.
Решение. По формуле (138), средняя орбитальная скорость первого компонента v1 = vr1 = c ( Δλ/λ)1 = 3·105·1,9·10-4; v1 = 57 км/с, Орбитальная скорость второго компонента v2 = vr2 = с (Δλ/λ)2 = 3·105·2,9·10-4; v2 = 87 км/с. Чтобы вычислить значения больших полуосей орбит компонентов, необходимо период обращения Р, равный периоду переменности, выразить в секундах. Так как 1д = 86400с, то Ρ = 3,953·86400c. Тогда, согласно (139), у первого компонента большая полуось орбиты
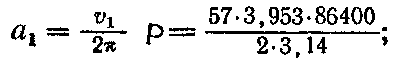
a1 = 3,10·106 км, а у второго а2 = (v2/2п) P = (v2/v1) a1, = (87/57)·3,10·106; a2=4,73·106 км,
и, по (140), большая полуось относительной орбиты a = a1 + a2 = 7,83·106; а = 7,83·106 км. Для вычисления суммы масс компонентов по формуле (125) следует выразить a в а. е. (1 а. е.= 149,6·106км) и Р — в годах (1 год=365д,3).
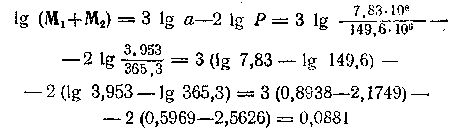
или М1 + М2 = 1,22 ~ 1,2. Отношение масс, по формуле (127),
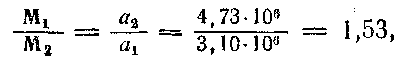
и тогда Μ1 ~ 0,7 и М2 ~ 0,5 (в массах Солнца).
|