| Тяжесть и тяготение |
|
Согласно закону всемирного тяготения, на поверхности сфероидального небесного тела с массой M и радиусом R гравитационное ускорение*
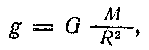 (92) (92)
а на поверхности Земли то же ускорение откуда, поделив первое равенство (92) на второе, получим:
где обязательно Μ выражается в массах Земли и R — в радиусах Земли, а В поле тяготения небесного тела на произвольном расстоянии от него гравитационное ускорение
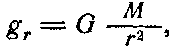
или, учитывая равенство (92),
В этой формуле r и R могут быть выражены в любых, но обязательно одинаковых единицах длины. * Ослабление g вращением тела здесь не рассматривается. |
Основы сферической и практической астрономии
Основы теоретической астрономии и небесной механики
Телескопы
Основы астрофизики и звездной астрономии
Прочее
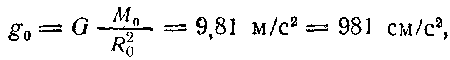
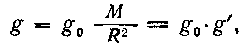 (93)
(93)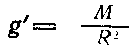
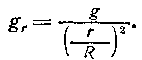 (94)
(94)