| Искусственные небесные тела |
|
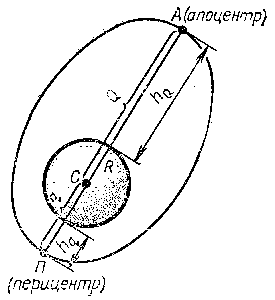
При запуске искусственных небесных тел им сообщается начальная скорость (скорость запуска) vн зависящая от рассчитанной орбиты. Начальная скорость сообщается космическим двигателем на некоторой высоте hн над поверхностью центрального тела (вокруг которого запускается спутник), г. е. от его центра на расстоянии r=R+hн, (74) где R — средний радиус этого тела. В частности, при запуске вокруг Земли R = 6371 км ~ 6370 км, что следует иметь в виду при решении задач этого раздела. Форма и размеры эллиптической орбиты искусственного спутника определяются целями запуска (рис. 8).
Рис. 8. Эллиптическая орбита искусственного снутпика
Центр центрального тела является одним из фокусов орбиты, а ее большая полуось
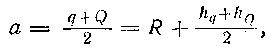
причем перицентрическое расстояние q = R+hq (76) и апоцентрическое расстояние Q = R+hQ, (77) где hq — наименьшая высота (высота перицентра) и hQ — наибольшая высота (высота апоцентра) искусственного спутника над поверхностью тела. Для искусственных спутников и орбитальных кораблей Земли hq — высота перигея, hQ — высота апогея, q — перигейиое расстояние и Q — апогейное расстояние. Эксцентриситет орбиты определяется формулой (35). Скорость искусственных небесных тел обычно выражается в км/с и вычисляется по формулам (40), (64) — (66) и (68) —(70). Периоды обращения искусственных спутников принято измерять в минутах, а их расстояния—в километрах, и поэтому третий закон Кеплера имеет вид
или
и
где M — масса центрального тела, выраженная в массах Земли. По параметрам обращения искусственного спутника можно вычислить массу центрального тела. Продолжительность полета искусственных спутников над полушарием центрального тела, расположенным под перицентром орбиты (перицентрийное полушарие),
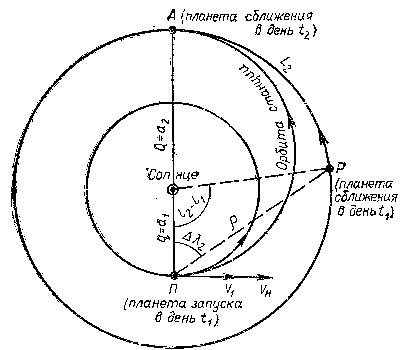
где Τ — период обращения спутника и е — эксцентриситет его орбиты. Над противоположным (апоцентрийным) полушарием спутник пролетает за интервал времени τ=T—t. (82) Формулы (75) — (82) вполне применимы и к движению естественных спутников планет. В полете с одной планеты к другой межпланетная станция (межпланетный корабль) становится спутником Солнца и движется в его поле тяготения по законам движения планет. Простейшей траекторией полета является полуэллиптическая, вершины (апсиды) которой касаются орбит планеты запуска (с нее производится запуск) и планеты сближения (к ней направляется станция). Пренебрегая в первом приближении наклонением и эллиптичностью планетных орбит, можно проводить расчеты по значениям их больших полуосей a1 (планеты запуска) и a2 (планеты сближения), заданных в астрономических единицах (а. е.). При полете к верхней планете (рис. 9) запуск станции осуществляется на ее перигельном расстоянии q=a1 (83) в прямом направлении; афелийное же расстояние станции Q=a2. (84)
Рис. 9. Простейшая орбита межпланетного корабля При направлении станции к нижней планете q = a2 и Большая полуось а гелиоцентрической орбиты межпланетной станции вычисляется по формуле (37), эксцентриситет орбиты — по формуле (35), а продолжительность полета, выраженная в годах,
где а — в астрономических единицах. При необходимости Δt переводится в сутки. Гелиоцентрическая скорость полета станции дается формулами (41), (64), (65) и (66). При запуске к верхней планете начальная гелиоцентрическая скорость Vн = Vq а при запуске к нижней планете Vн = VQ причем в эту скорость Vн входит орбитальная (в рассматриваемом здесь простейшем случае—круговая) скорость V1 планеты запуска. Следовательно, чтобы межпланетная станция вышла на расчетную гелиоцентрическую орбиту, необходимо сообщить ей дополнительную скорость Vд = Vн - V1 (86) Но, чтобы покинуть планету запуска, станция должна еще преодолеть ее притяжение, на что требуется кинетическая энергия wп — вторая космическая (критическая) скорость на поверхности этой планеты. Поэтому скорость запуска vн станции с планеты, называемая также начальной плане-тоцентрической скоростью, найдется из равенства
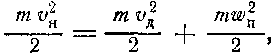
откуда
День запуска t1 межпланетной станции не может быть произвольным и выбирается по подходящей конфигурации Δλ2 планеты сближения Ρ (см. рис. 9), иначе станция придет в намеченный район встречи либо раньше, либо позже планеты. У планеты сближения с сидерическим периодом обращения Т2 среднее суточное движение.
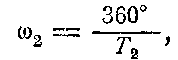
и за найденную по формуле (85) продолжительность полета станции Δt (выраженную в сутках) планета должна прийти в район встречи A, пройдя по своей орбите путь
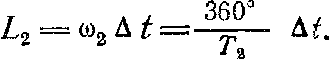
Следовательно, в день t1 старта межпланетной станции разность гелиоцентрической долготы планеты сближения (l2) и планеты запуска (l1) должна быть l2- l1 = 180°—L2 = 180° — ω2Δt (88) и по этой разности нетрудно найти в астрономическом календаре-ежегоднике на текущий год подходящий день l1. В этот день расстояние между планетами
а конфигурация Δλ2 планеты сближения вычисляется либо из равенства
либо по формуле
Легко видеть, что при L2 < 180° найденная элонгация будет западной, а при L2 > 180° — восточной. Очевидно, межпланетная станция подойдет к планете сближения в день t2 = t1 + Δt. |
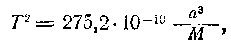 (78)
(78) 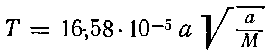 (79)
(79)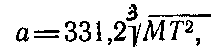 (80)
(80)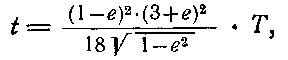 (81)
(81)
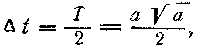 (85)
(85)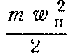
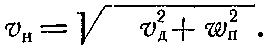 (87)
(87)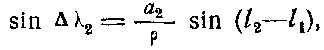 (90)
(90) 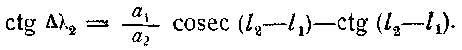 (91)
(91)