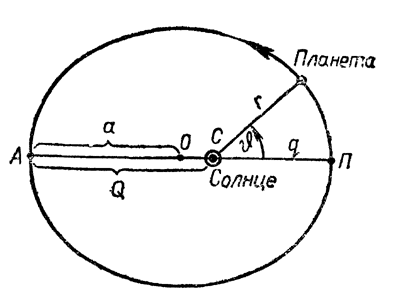
Планеты обращаются вокруг Солнца по эллиптиче­ским орбитам, в одном, общем фокусе которых находит­ся Солнце. В первом приближении можно считать, что орбиты больших планет (кроме Плутона) лежат в одной плоскости. Большая полуось α орбиты (рис. 4) опреде­ляет размеры, а эксцентриситет е — степень вытянутости орбиты.

Рис. 4. Эллиптическая орбита

Радиус-вектор r планеты определяется уравне­нием эллипса

                         (34)

и меняется в пределах от перигельного расстояния

q= СП = α (1—е),                                   (35)

когда истинная аномалия θ=0°, до афелийного расстоя­ния

Q = CA = α (l+e)                                      (36)

при θ =180°.

Средним расстоянием планеты от Солнца является большая полуось ее орбиты

                            (37)

Расстояния между планетами и расстояния планет от Солнца обычно выражаются в астрономических едини­цах (а. е.), но иногда и в километрах из расчета, что 1 а. е. = 149,6·10⁶ км.

Звездные, или си­дерические, периоды обращения Т₁ и Т₂ двух планет связаны с их средними расстоя­ниями а₁ и а₂ от Солн­ца третьим законом Кеплера

                (38)

Если Τ дается в го­дах   и   а — в   астроно­мических единицах, то, принимая для Земли T₀ = 1 год и а₀ = 1 а. е., получим для любой планеты

Т² = а³                                   (39)

Средняя орбитальная, или круговая, скорость планеты

                (40)

всегда выражается в км/с. Так как обычно а задается в астрономических единицах (1 а. е.= 149,6·10⁶ км) и T— в годах (1 год=31,56·10⁶ с), то

 

 

Заменив Τ из формулы (39), получим: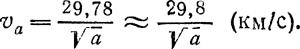

средняя продолжительность синодического периода обращения S планеты связана с сидерическим периодом Τ уравнением синодического движения:

для  верхних планет

для нижних планет

где Т₀ — сидерический период обращения Земли, равный 1 звездному году.

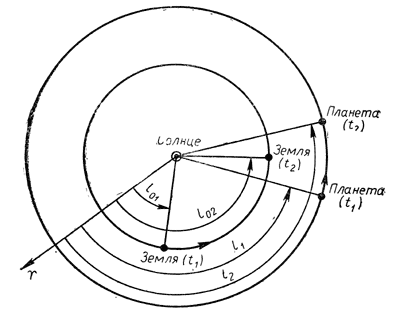
Средний синодический период обращения позволяет вычислить примерную дату   t₂ очередного   наступления определенной конфигурации планеты по известной дате t₁ такой же конфигурации, так как

t₂ ~ t₁ + S.         (44)

Любые планетные конфигурации и даты их наступле­ния могут быть вычислены по гелиоцентрической долго­те l планет, отсчитываемой в плоскости эклиптики от точки весеннего равноденствия γ в прямом направле­нии, т. е. против вращения часовой стрелки. Пусть в не­который день года t₁ гелиоцентрическая долгота верхней планеты l1 а гелиоцентрическая долгота Земли l₀₁ (рис. 5). Планета за средние сутки проходит по орбите дугу ω = 360°/T (среднее суточное движение планеты), а Земля — дугу ω₀=360°/T₀ (среднее суточное движение Земли), где Τ и Т₀ выражены в средних сутках, причем Т > Т₀ и ω < ω₀.

В день t₂ искомой конфигурации гелиоцентрическая долгота планеты 

l2 = l1 + ω(t2- t1) = l1 + ω Δt      (45)

Рис. 5. Гелиоцентрическая долгота

а Земли

l₀₂ = l₀₁ + ω₀ (t₂—t₁) = l₀₁+ω·Δt,        (46)

откуда,  обозначив   ω₀—ω = Δω   и   (l₀₂—l₀₁) — (l₂—l₁) = L, получим:

Δt=L/Δω                  (47)

и

t2 = t1+Δt.             (48)

При вычислении конфигураций нижних планет Δω = ω—ω₀.

Наибольшие сближения с Землей планет, обращаю­щихся по заметно вытянутым орбитам, повторяются че­рез целые числа m и n средних синодических S и сидери­ческих Τ периодов обращения, поскольку

mS = nT.                (49)

Эта же формула позволяет установить периодичность великих противостояний планет.