Выяснить обстоятельства полета межпланетного корабля с Венеры к Юпитеру. Среднее гелиоцентриче­ское расстояние Юпитера — 5,203 а. е., а Венеры — 0,723 а. е. Критическая (вторая космическая) скорость на поверхности Венеры 10,36 км/с; среднее суточное движение Юпитера 0°,0831.

Данные: планета запуска, Венера, а₁ = 0,723, а.е., w_п = 10,36 км/с; планета сближения,, Юпитер, а₂ = 5,203 а. е., ω₂ = 0°,831 ~ 5' (в сутки).

Решение. Изображаем орбиты обеих планет и ге­лиоцентрическую орбиту межпланетного корабля (см. рис. 9). Поскольку корабль стартует с нижней планеты к верхней, то запуск происходит в перигелии, и, согласно формулам (83), (84), (75), (35) и (85), перигельное расстояние корабля q = a₁ = 0,723 а. е., афелийное рас­стояние

Q = a₂ = 5,203 а. е., большая, полуось орбиты

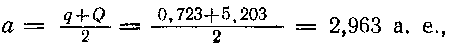
эксцентриситет орбиты

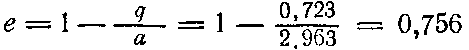
и продолжительность полета к Юпитеру

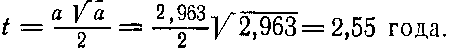
По формуле (41) гелиоцентрическая круговая ско­рость корабля

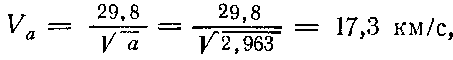
а по (65) —скорость в перигелии, она же начальная ге­лиоцентрическая скорость корабля,

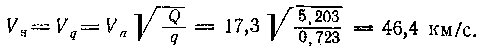
Так как орбитальная скорость Венеры

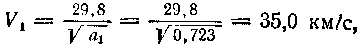
то, согласно (86), дополнительная скорость

откуда, по (87), скорость запуска корабля с Венеры

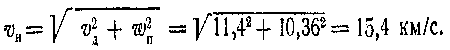
За промежуток времени Δt = 2,55 года = 2,55·365 сут Юпитер пройдет по своей орбите путь

L₂ = ω₂Δt =  0°,0831·2,55·365 = 77°,4,

и поэтому, по (88), в день старта корабля разность ге­лиоцентрической долготы Юпитера и Венеры

l₂—l₁  = 180°—L₂= 180°—77°,4 = 102°,6,

а конфигурация Δλ₂ Юпитера, видимая с Венеры, нахо­дится по формуле (91):

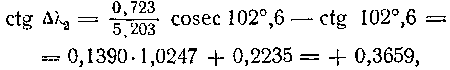
откуда Δλ₂ = 69°,9. Поскольку L₂ = 77°,4 < 180°, то найден­ная конфигурация представляет собой западную элонга­цию. Этот же результат получается и по формулам (89) и  (90).